最小生成树(Minimum Spanning Tree)是图论中的重要概念,用于寻找连接图中所有节点的最优路径。本文将详细介绍最小生成树算法的原理、常见实现方法,以及在实际应用中的重要性和应用场景。
最小生成树原理
最小生成树是指在一个加权无向连通图中,找到一棵生成树,使得树上所有边的权值之和最小,且连接所有节点。最小生成树算法的原理基于贪心策略,通过按照特定规则选择边来构建最小生成树,确保每次选择的边都是当前权值最小的边,并且不会形成环路。
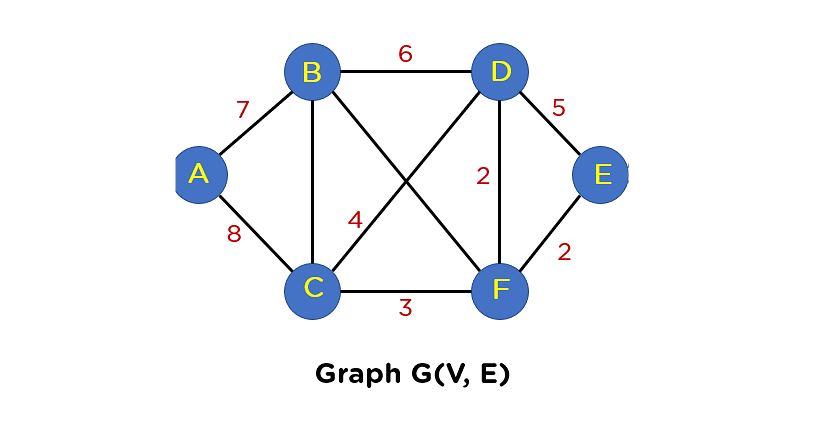
常见的最小生成树算法
- 普里姆(Prim)算法:从一个起始节点开始,逐步扩展生成树,每次选择与生成树连接的权值最小的边,并将其加入生成树的集合中。通过不断扩展生成树,直到所有节点都被连接为止。代码如下:
#include <stdio.h>
#include <stdbool.h>
#define INF 9999
#define V 5
int graph[V][V] = {
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
int minKey(int key[], bool mstSet[])
{
int min = INF, min_index;
for (int v = 0; v < V; v++)
{
if (mstSet[v] == false && key[v] < min)
{
min = key[v];
min_index = v;
}
}
return min_index;
}
void printMST(int parent[], int n)
{
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
{
printf("%d - %d \t%d\n", parent[i], i, graph[i][parent[i]]);
}
}
void primMST()
{
int parent[V];
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++)
{
key[i] = INF;
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++)
{
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
{
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
{
parent[v] = u;
key[v] = graph[u][v];
}
}
}
printMST(parent, V);
}
int main()
{
primMST();
return 0;
}- 克鲁斯卡尔(Kruskal)算法:将图中的所有边按照权值从小到大排序,然后依次选择权值最小的边,如果该边的两个节点不在同一个连通分量中,则将其加入生成树的集合中。通过不断选择边,直到生成树包含了所有节点。 代码如下:
#include <stdio.h>
#include <stdlib.h>
#define MAX_EDGES 50
typedef struct
{
int source, destination, weight;
} Edge;
typedef struct
{
int parent;
int rank;
} Subset;
typedef struct
{
int V, E;
Edge edges[MAX_EDGES];
} Graph;
Graph* createGraph(int V, int E)
{
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->V = V;
graph->E = E;
return graph;
}
int find(Subset subsets[], int i)
{
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(Subset subsets[], int x, int y)
{
int root_x = find(subsets, x);
int root_y = find(subsets, y);
if (subsets[root_x].rank < subsets[root_y].rank)
subsets[root_x].parent = root_y;
else if (subsets[root_x].rank > subsets[root_y].rank)
subsets[root_y].parent = root_x;
else
{
subsets[root_y].parent = root_x;
subsets[root_x].rank++;
}
}
int compareEdges(const void* a, const void* b)
{
Edge* edge1 = (Edge*)a;
Edge* edge2 = (Edge*)b;
return edge1->weight - edge2->weight;
}
void kruskalMST(Graph* graph)
{
int V = graph->V;
Edge result[V];
int e = 0;
int i = 0;
qsort(graph->edges, graph->E, sizeof(Edge), compareEdges);
Subset* subsets = (Subset*)malloc(V * sizeof(Subset));
for (int v = 0; v < V; v++)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
while (e < V - 1 && i < graph->E)
{
Edge next_edge = graph->edges[i++];
int x = find(subsets, next_edge.source);
int y = find(subsets, next_edge.destination);
if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
}
printf("Following are the edges in the constructed MST:\n");
for (i = 0; i < e; ++i)
printf("%d -- %d == %d\n", result[i].source, result[i].destination, result[i].weight);
}
int main()
{
int V = 4; // 图中的节点数
int E = 5; // 图中的边数
Graph* graph = createGraph(V, E);
// 添加边
graph->edges[0].source = 0;
graph->edges[0].destination = 1;
graph->edges[0].weight = 10;
graph->edges[1].source = 0;
graph->edges[1].destination = 2;
graph->edges[1].weight = 6;
graph->edges[2].source = 0;
graph->edges[2].destination = 3;
graph->edges[2].weight = 5;
graph->edges[3].source = 1;
graph->edges[3].destination = 3;
graph->edges[3].weight = 15;
graph->edges[4].source = 2;
graph->edges[4].destination = 3;
graph->edges[4].weight = 4;
kruskalMST(graph);
return 0;
}
最小生成树的重要性和应用场景
- 网络设计:在计算机网络中,最小生成树用于设计网络拓扑,确保网络中的所有节点都能够相互通信,并且连接的成本最小。通过最小生成树算法,可以构建高效的网络结构,提高通信的效率和稳定性。
- 电力传输:在电力传输网络中,最小生成树可以帮助确定最优的输电线路,以最大程度地减少能量损耗和成本。通过选择最佳的传输路径,可以提高电力传输的效率和可靠性。
- 物流规划:在物流领域,最小生成树可以帮助确定最优的供应链路线,以最小化物流成本和时间。通过应用最小生成树算法,可以优化物流规划,提高运输效率和降低成本。
总结
最小生成树是连接图中所有节点的最优路径,通过贪心策略和选择权值最小的边来构建。普里姆和克鲁斯卡尔算法是常见的最小生成树算法。最小生成树在网络设计、电力传输和物流规划等领域具有重要应用。通过应用最小生成树算法,我们能够找到经济高效的连接方案,实现资源的最优利用和成本的最小化。无论是构建网络拓扑、优化电力传输还是规划物流路径,最小生成树算法都发挥着不可或缺的作用。

如果你对编程知识和相关职业感兴趣,欢迎访问编程狮官网(https://www.w3cschool.cn/)。在编程狮,我们提供广泛的技术教程、文章和资源,帮助你在技术领域不断成长。无论你是刚刚起步还是已经拥有多年经验,我们都有适合你的内容,助你取得成功。





